美女美女大片黄a大片-美女免费黄色-美女免费黄网站-美女免费精品视频在线观看-特级xxxxx欧美-特级a级毛片

　　《新型顆粒增強金屬玻璃復合材料的拉伸增韌機制》一文利用有限元方法探究了顆粒體積分數、顆粒的應變硬化指數、顆粒的間距以及網狀結構對新型非晶合金復合材料即金屬玻璃基復合材料強度和韌性的影響。上述工作的作者是河海大學力學與材料學院的邱昆，通信作者是南京航空航天大學航空宇航學院姜云鵬教授。

　　金屬玻璃是合金熔體在急速冷卻條件下形成的一種新型亞穩態材料。它有帶狀、絲狀和塊體等形式，具有廣闊的應用前景。

　　金屬玻璃內部原子接近長程無序、短程有序，不存在位錯、晶界等缺陷決定了金屬玻璃有高強度、高硬度、高彈性極限等優良性能，但在室溫下它呈現非均勻變形，塑性變形也局限于極窄的剪切帶內，限制了它實際應用的范圍。

　　作者利用自由體積模型編寫材料子程序，同時建立代表性體積單元模型，后分析了顆粒對MGCs的影響機制和顆粒體積分數、顆粒應變硬化指數、顆粒的間距、網狀結構對MGCs拉伸塑性的影響。

　　1、計算模型

　　1.1金屬玻璃基體本構方程

　　金屬玻璃的基本變形機制是剪切帶的形成和演化。剪切帶形成與局部結構次序的演化有關，它是應變軟化導致局部化變形的結果。為使本構關系具有捕捉剪切帶的能力，自由體積模型引入自由體積作為狀態變量。該模型假設在純剪切情況下宏觀塑性流動是凈原子在外加應力方向上以躍遷的形式出現。

　　金屬玻璃塑性流動方程如下:

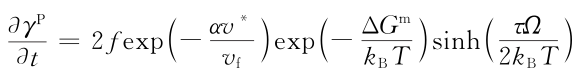
　　在外加應力情況下，應力驅動產生自由體積和結構弛豫湮滅自由體積相互競爭使結構重排。純自由體積增加如下：

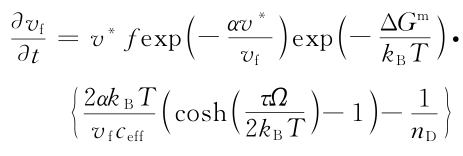
　　在多軸應力狀態下，自由體積演變方程為：

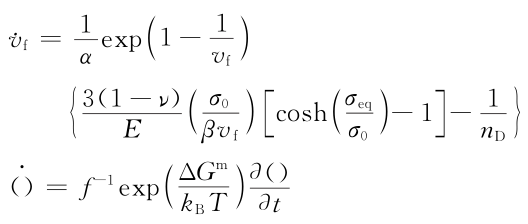
　　在上述自由體積模型中，剪切帶演變被看成是內部狀態變量，也就是在方程式中給出的標準自由體積Vf。自由體積場的演變很大程度上依賴于原來的應力狀態和當時的自由體積場。

　　1.2顆粒的本構方程

　　顆粒滿足J2塑性流動理論如下：

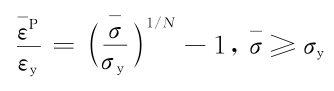
　　2、有限元計算模型

　　為了用有限元計算展現復合材料的微觀機制，建立一個代表性體積單元模型來描述復合材料的宏觀力學性能。

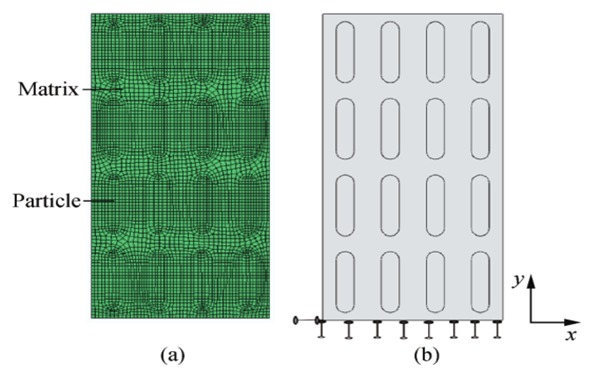
　　圖1：顆粒體積分數為30的MGCs的RVE模型

　　從本質上看，MGCs中包含著軟硬不均勻區域，這些結構的不均勻性將會導致剪切轉變區匯集和隨后剪切帶的形成與擴展。

　　3、結果討論

　　3.1不同顆粒體積分數對MGCs的影響

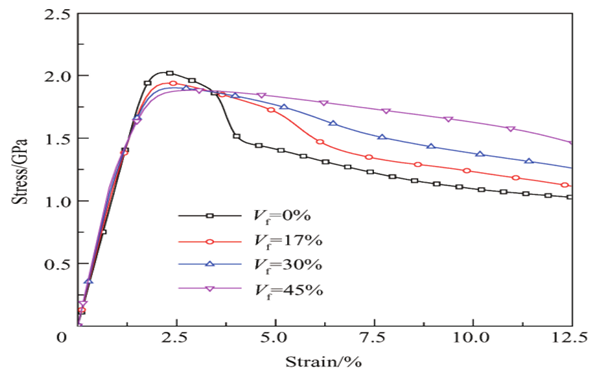
　　圖2：顆粒體積分數不同的MGCs的應力-應變曲線

　　從圖2可以看出，隨著體積分數的增加，復合材料的塑性提高但犧牲了部分強度。

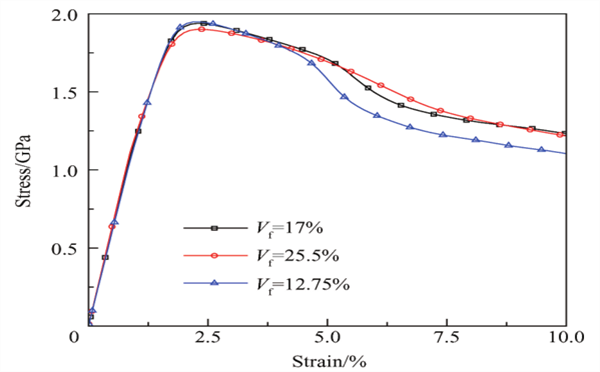
　　圖3：顆粒大小相同、顆粒體積含量不同的MGCs的應力-應變曲線

　　從圖3可以看出，隨著顆粒體積分數的增加，復合材料的塑性增加。

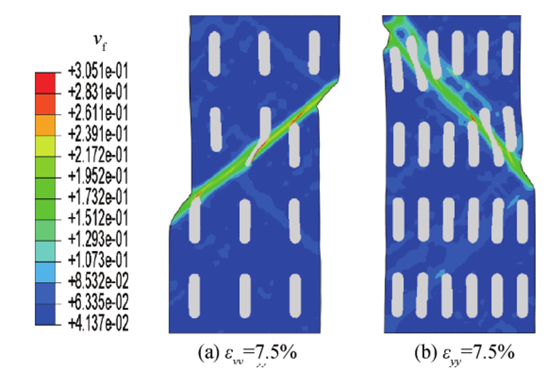
　　圖4：MGCs中顆粒體積分數為12.75 和25.5 時的剪切帶云圖

　　從圖4中可以看出，體積分數為25.5時，主剪切帶在穿過顆粒的同時，也出現繞著顆粒擴展，使基體的應力下降緩慢，塑性增強，同時與體積分數為12.75時相比，開始出現部分層狀次級剪切帶和剪切帶交割，因此吸收更多變形能，韌性提高。

　　3.2 不同顆粒間距對MGCs的影響

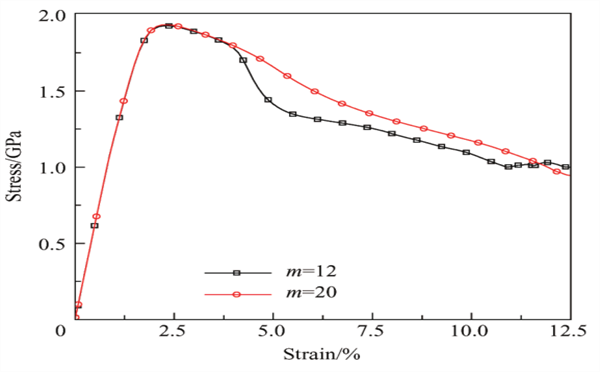
　　圖5：MGCs 中不同顆粒間距時的應力-應變關系

　　通過改變顆粒的大小獲得不同的間距。從圖中可以看出，隨著顆粒間距的減小即顆粒數的增加，復合材料的強度變化不明顯，但塑性卻有明顯的增加。

　　3.3 不同硬化指數對MGCs的影響

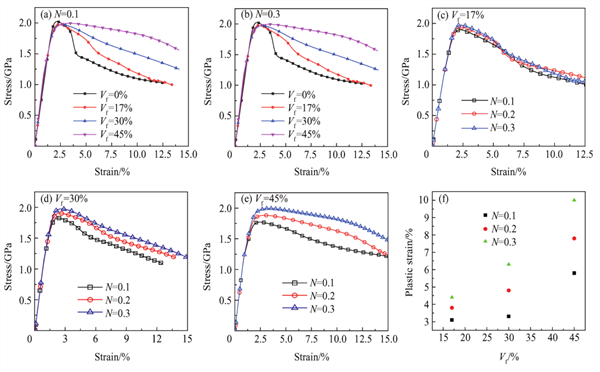
　　圖6：MGCs中顆粒不同硬化指數時的應力-應變關系

　　對比硬化指數N =0.1的應力-應變曲線所示)和硬化指數N=0.3的應力應變曲線所示)，都有5個階段出現，而且顆粒體積分數提高大時，應力強度降低，塑性應變增強。

　　但是硬化指數從N=0.1到N=0.3過程中，通過圖6~6可知，都有一個相同的規律，即硬化指數高時塑性應變提高，而且大應力強度提高。

　　3.4不同微結構對MGCs的影響

　　由顆粒的間距變化，聯想到高體積分數顆粒會排布成類似絲瓜狀的網狀結構或者直接在復合材料中加入這種網狀結構，增韌效果可能更好。

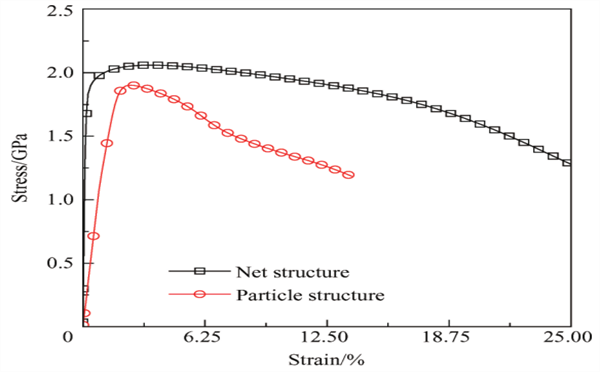
　　圖7：MGCs中顆粒不同結構排列下MGCs的應力-應變關系

　　可以看出，網狀結構的排列與顆粒豎直排列的結構相比，復合材料的強度不僅得到提高，彈性模量也增加，塑性也得到很大的增強。從圖7~的變化過程中可以看出，網狀結構隨著荷載的增大，幾乎是均勻變形，直到后自由體積含量達到飽和，結構遭到破壞。因此彈性比提高，吸收變形能力提高，韌性增強。

　　4、結論

　　隨著顆粒體積分數的提高，金屬玻璃復合材料的塑性增強，但犧牲了部分強度，尤其當體積分數達到45時，材料的塑性得到很大的提高。

　　隨著顆粒間距的減小，MGCs的強度變化不大，但塑性得到了增強。

　　隨著顆粒硬化指數從0.1增大到0.3，MGCs的塑性和強度都得到提高。主要原因在于高強度顆粒更加有效地阻礙剪切帶的快速擴展。

　　顆粒結構如果能用同種材料的網狀結構進行替代，可以發現，網狀結構更能引起復合材料的均勻變形，進而增大復合材料的強度和韌性。